Hello everyone! I hope y’all enjoyed the last two articles about the Loss function! Today, we are going to tackle another pivotal aspect of Machine Learning: Embeddings! So let’s get right into it and see for ourselves what is embedding in Machine Learning.
Embedding in Machine Learning: a new way to look at things
We are going to start with quite a formal definition: embedding is a method used to represent discrete variables as continuous vectors. This is all well and good, but what does it mean? As always, let’s start with an example.
Let’s say we have a shoes’ retailer website, and we want to categorize them based on their model and make, so that we can recommend our customers what to buy based on their purchase history. We could have hundreds of users and hundreds of shoes models… What would our data look like? Let’s assume we put all the users and all of our shoes in order in a table like so:
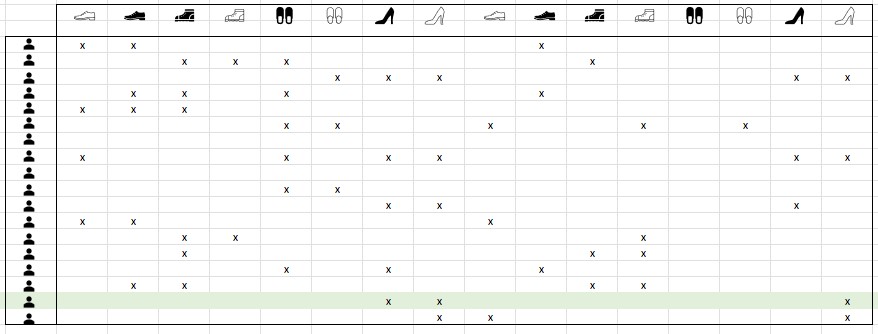
Now, this is a perfectly acceptable way to represent our data. We could then represent each line as a one-hot-encoded vector. Let’s take as an example the green line, and see what the one-hot-encoded vector for that line:
Y = [0, 0, 0, 0, 0, 0, 0, 1, 1, 0, 0, 0, 0, 0, 0, 1]
As you can see, we could definitely represent data that way. However, let’s imagine we have hundreds or even thousands of shoes in our catalog, and thousands of users: one-hot-encoded vectors would become a bit cumbersome to manage, and quite memory intensive.
One better way to represent this data is by using embeddings. What we could do is use the index – starting from zero – of the shoes’ column, and put that index in our vector instead of representing all columns with either a zero or a one. We can then efficiently represent the sparse vector as just the shoes the user bought. Our data would then look something like this:
Y = [7, 8, 15]
Much more convenient!
This way, we can represent our data in a less sparse, less dispendious way. In this case, we are basically building a dictionary mapping each feature to an integer from 0 to the number of shoes-1.
Embedding in Machine Learning
So, in the light of our previous example, let’s now have a look at another way to define embedding in Machine Learning:
An embedding is a relatively low-dimensional space into which you can translate high-dimensional vectors. Embeddings make it easier to do machine learning on large inputs like sparse vectors representing words. Ideally, an embedding captures some of the semantics of the input by placing semantically similar inputs close together in the embedding space. An embedding can be learned and reused across models.
– Google’s Machine Learning Crash Course
What this means is that we can actually use embeddings to represent our data in a d_dimensional space, where d is the number of dimensions our embedding matrix has. Every data point is then represented by a vector of length d, and similar data points are going to be clustered close to one another.
Each dimension represents a different aspect or feature of our data; in the case of our shoes, it could be whether a shoe is elegant or not, quality, popularity, price point… and so on. Every shoe would then become a d-dimensional point, and the value at dimension d represents the degree to which the shoe fits that aspect.
Now, we usually only give examples of embeddings in two or three-dimensional spaces, simply because we can easily represent them for human comprehension, but embeddings can have hundreds of dimensions.
I will give you an example later on, but if you want to have a look right now, look at this article by Will Koehrsen.
Now what’s even more fun is that we can learn embeddings from data!
An Embedding Layer Within a Neural Network
Now that we know what embedding in Machine Learning, let’s see how we actually use them in a Neural Network. As we said, embeddings can be learned from data, and there is no additional training process needed. We will just add a hidden layer, our embedding layer, that will have one unit per embedding dimension.
These units will find out a way to organize the items in the d-dimensional space to optimize the task at hand.
Through back propagation, our network would then learn the correct embeddings like any other training.
But let’s pause for a second to talk about our training data. What would our dependent and independent variables be? What would we use to label our data? Well, in our example of shoes recommendation, what we would do is basically split the data we have for each user. Let’s say a customer has purchased 10 pairs of shoes. We would only use seven as our independent variable, and use the remaining three as our label. It makes perfect sense, since the customer has actually purchased those three pair of shoes, so they would make a perfect suggestion!
Now, how do we get spacial representation from our input data and embedding layer? It’s quite easy actually: the edge weights between a data point (one shoe model, for example) and the hidden embedding layer can be considerate as coordinate values in our d-dimensional space.
When we are done training your neural network, those edges are weights, each edge has a real value associated with it, and that’s our embedding.
Choosing the Dimension of Embedding in Machine Learning
So one last little thing to note. We need to choose how many dimensions our embeddings will have. The more dimensions our embeddings have, the more accurately they can represent the relationships between input values.
However, having more dimensions means we have a higher chance of overfitting and slower training.
The Google course I linked above suggests this empirical rule-of-thumb (to be tuned using the validation data): embedding dimensions should be equal to the fourth root of the number of possible values.
And there you have it! I hope you enjoyed it, and see you in a bit!



